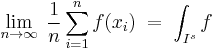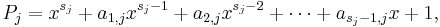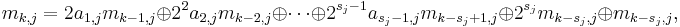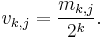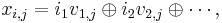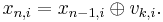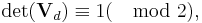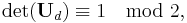Sobol sequence
Sobol sequences (also called LPτ sequences or (t, s) sequences in base 2) are an example of quasi-random low-discrepancy sequences. They were first introduced by I.M.Sobol'[note 1] in 1967.[1]
These sequences use a base of two to form successively finer uniform partitions of the unit interval, and then reorder the coordinates in each dimension.
Contents[hide] |
Good distributions in the s-dimensional unit hypercube
Let Is = [0,1]s be the s-dimensional unit hypercube and f a real integrable function over Is. The original motivation of Sobol' was to construct a sequence xn in Is so that
and the convergence be as fast as possible.
It is more or less clear that for the sum to converge towards the integral, the points xn should fill Is minimizing the holes. Another good property would be that the projections of xn on a lower-dimensional face of Is leave very few holes as well. Hence the homogeneous filling of Is does not qualify ; because in lower-dimensions many points will be at the same place, therefore useless for the integral estimation.
These good distributions are called (t,m,s)-nets and (t,s)-sequences in base b. To introduce them, define first an elementary s-interval in base b a subset of Is of the form
![\prod_{j=1}^s \left[ \frac{a_j}{b^{d_j}}, \frac{a_j%2B1}{b^{d_j}} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/56021f9c0fa740d9662ef678ea20a7ca.png) , where aj, dj are integers and aj<dj for all j in {1, ...,s}
, where aj, dj are integers and aj<dj for all j in {1, ...,s}
Given 2 integers 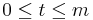 , a (t,m,s)-net in base b is a sequence xn of bm points of Is such that
, a (t,m,s)-net in base b is a sequence xn of bm points of Is such that 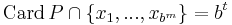 for all elementary interval P in base b of hypervolume λ(P) = bt-m.
for all elementary interval P in base b of hypervolume λ(P) = bt-m.
Given a non-negative integer t, a (t,s)-sequence in base b is an infinite sequence of points xn such that for all integers 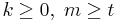 , the sequence
, the sequence 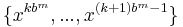 is a (t,m,s)-net in base b.
is a (t,m,s)-net in base b.
In his article, Sobol' spoke of Πτ-meshes and LPτ sequences, which are (t,m,s)-nets and (t,s)-sequences in base 2 respectively. The terms (t,m,s)-nets and (t,s)-sequences in base b (also called Niederreiter sequences) where coined in 1988 by H. Niederreiter.[2] The term Sobol sequences was introduced in late English-speaking papers in comparison with Halton, Faure and other low-discrepancy sequences.
Construction of the Sobol sequence
The algorithm for generating Sobol sequences is clearly explained in Bratley and Fox, Algorithm 659[3]
To generate the j-th component of the points in a Sobol' sequence, we need to choose a primitive polynomial of some degree sj over the field GF(2)
where the coefficients a1,j, a2,j, ..., asj−1,j are either 0 or 1. The error bounds for Sobol' sequences given in [1] indicate that we should use primitive polynomials of as low a degree as possible.
A sequence of positive integers {m1,j, m2,j, ...} are defined by the recurrence relation
where  is the bit-by-bit exclusive-or operator. The initial values m1,j, m2,j, ..., msj,j can be chosen freely provided that each mk,j, 1 ≤ k ≤ sj, is odd and less than 2k.
is the bit-by-bit exclusive-or operator. The initial values m1,j, m2,j, ..., msj,j can be chosen freely provided that each mk,j, 1 ≤ k ≤ sj, is odd and less than 2k.
The so-called direction numbers {v1,j, v2,j, . . .}[note 2] are defined by
Then xi,j , the j-th component of the i-th point in a Sobol' sequence, is given by
where ik is the k-th binary digit of i = (. . . i3i2i1)2. Here the notation (·)2 denotes the binary representation of numbers.
A fast algorithm for the construction of Sobol sequences
A more efficient Gray code implementation was proposed by Antonov and Saleev [4]
As for the generation of Sobol' numbers, they are clearly aided by the use of Gray code 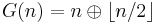 instead of n for constructing the n-th point draw.
instead of n for constructing the n-th point draw.
Suppose we have already generated all the Sobol' sequence draws up to n − 1, and kept in memory the values xn−1,j for all the required dimensions. Since the Gray code G(n) differs from that of the preceding one G(n − 1) by just a single, say the k-th, bit (which is a rightmost bit of n − 1), all that needs to be done is a single XOR operation for each dimension in order to propagate all of the xn−1 to xn, i.e.
Additional uniformity properties
Sobol’ introduced additional uniformity conditions known as property A and A’.[5]
Definition. A low-discrepancy sequence is said to satisfy Property A if for any binary segment (not an arbitrary subset) of the d-dimensional sequence of length 2d there is exactly one draw in each 2d hypercubes that result from subdividing the unit hypercube along each of its length extensions into half.
Definition. A low-discrepancy sequence is said to satisfy Property A’ if for any binary segment (not an arbitrary subset) of the d-dimensional sequence of length 4d there is exactly one draw in each 4d hypercubes that result from subdividing the unit hypercube along each of its length extensions into four equal parts.
There are mathematical conditions that guarantee properties A and A'.
Theorem. The d-dimensional Sobol sequence possesses Property A iff
where Vd is the d × d binary matrix defined by
 ,
,
with vk,j,m denoting the m-th digit after the binary point of the direction number vk,j = (0.vk,j,1vk,j,2 . . .)2.
Theorem. The d-dimensional Sobol sequence possesses Property A' iff
where Ud is the 2d × 2d binary matrix defined by
 ,
,
with vk,j,m denoting the m-th digit after the binary point of the direction number vk,j = (0.vk,j,1vk,j,2 . . .)2.
Tests for properties A and A’ are independent. Thus it is possible to construct the Sobol’ sequence which satisfies both properties A and A’ or only one of them.
The initialization of Sobol' numbers
To construct a Sobol' sequence a set of direction numbers vi,j needs to be selected. There is some freedom in the selection of initial direction numbers.[note 3] Therefore, it is possible to receive different realisations of the Sobol' sequence for selected dimensions. A bad selection of initial numbers can considerably reduce the efficiency of Sobol sequences when used for computation.
Arguably the easiest choice for the initialisation numbers is just to have the l-th leftmost bit set, and all other bits to be zero, i.e. mk,j = 1 for all k and j. This initialisation is usually called unit initialisation. However, such a sequence fails the test for Property A and A’ even for low dimensions and hence this initialisation is bad.
Good initialisation numbers for different numbers of dimensions are provided by several authors.
Sobol' provides initialisation numbers for dimensions up to 51.[6] The same set of initialisation numbers is used by Bratley and Fox.[3]
Peter Jäckel provides initialisation numbers up to dimension 32 in his famous book "Monte Carlo methods in finance".[7]
Other implementations are available as C, Fortran 77, or Fortran 90 routines in the popular Numerical Recipes collection of software (for example, see Press et al.[8]).
Initialisation numbers for high dimensions are available on Joe and Kuo.[9]
There are also some commercial Sobol' sequence generators available, for example see [10] or.[11]
See also
Notes
- ^ In Cyrillic as "Илья Меерович Соболь", as per [1].
- ^ In some papers numbers mk,j also can be referred as direction numbers.
- ^ These numbers are usually called initialisation numbers
References
- ^ a b Sobol',I.M. (1967), "Distribution of points in a cube and approximate evaluation of integrals". Zh. Vych. Mat. Mat. Fiz. 7: 784–802 (in Russian); U.S.S.R Comput. Maths. Math. Phys. 7: 86–112 (in English).
- ^ Niederreiter, H. (1988). "Low-Discrepancy and Low-Dispersion Sequences", Journal of Number Theory 30: 51–70.
- ^ a b Bratley, P. and Fox, B. L. (1988), "Algorithm 659: Implementing Sobol’s quasirandom sequence generator". ACM Trans. Math. Software 14: 88–100.
- ^ Antonov, I.A. and Saleev, V.M. (1979) "An economic method of computing LPτ-sequences". Zh. Vych. Mat. Mat. Fiz. 19: 243–245 (in Russian); U.S.S.R Comput. Maths. Math. Phys. 19: 252–256 (in English).
- ^ Sobol',I.M. (1976) "Uniformly distributed sequences with an additional uniform property". Zh. Vych. Mat. Mat. Fiz. 16: 1332–1337 (in Russian); U.S.S.R Comput. Maths. Math. Phys. 16: 236–242 (in English).
- ^ Sobol', I.M. and Levitan, Y.L. (1976). "The production of points uniformly distributed in a multidimensional cube" Tech. Rep. 40, Institute of Applied Mathematics, USSR Academy of Sciences (in Russian).
- ^ Jäckel, P. (2002) "Monte Carlo methods in finance". New York: Wiley
- ^ Press, W.H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (1992) "Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd ed." Cambridge University Press, Cambridge, U.K.
- ^ http://web.maths.unsw.edu.au/~fkuo/sobol/
- ^ http://www.broda.co.uk
- ^ http://www.nag.co.uk/
External links
- Collected Algorithms of the ACM (See algorithms 647, 659, and 738.)
- Collection of Sobol sequences generator programming codes